线性变换与仿射变换
线性变换的性质:对于 n 维向量的所有线性变换都可以用 n * n 矩阵表示。常见的缩放和旋转都是线性变换。线性变换满足以下式子:
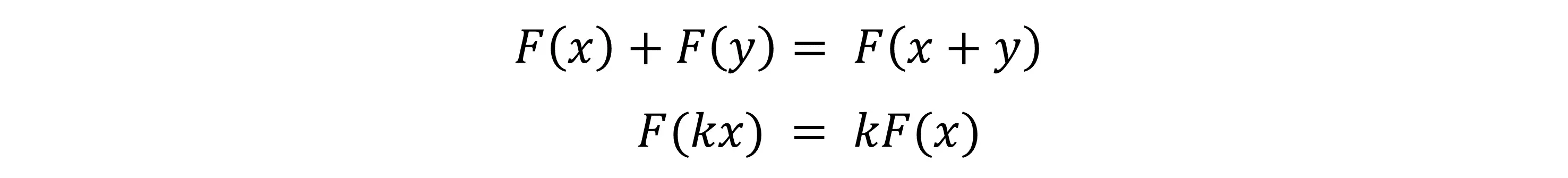
平移不是线性变换。线性变换结合平移,称之为仿射变换(Affine transform),对于 3 维向量的仿射变换通常可以用 4 维矩阵表示,那么向量也需要 4 维的表示方式;本文对于向量的表示采取列向量的形式,且遵循右手定则。区别方向向量和点向量,方向向量代表一个方向,表示为(x, y, z, 0),点向量表示空间中的一个点,表示为(x, y, z, 1);
平移变换
设平移矢量为 t,那么平移变换矩阵表示如下:
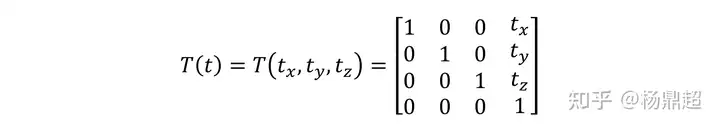
平移操作是针对点而言的,所以分别对方向(x, y, z, 0)和点(x, y, z, 1)操作会得到不同的结果:

平移变换的逆就相当于平移回去,即:
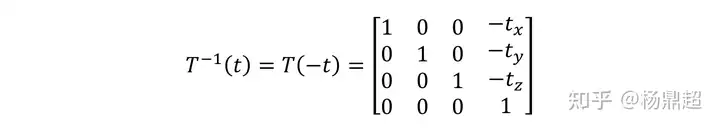
旋转变换
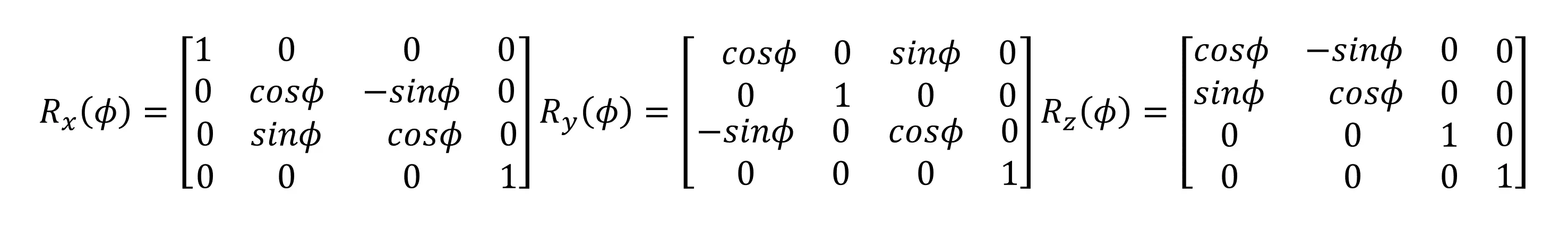
旋转矩阵的逆和平移类似,就是旋转回去,即:
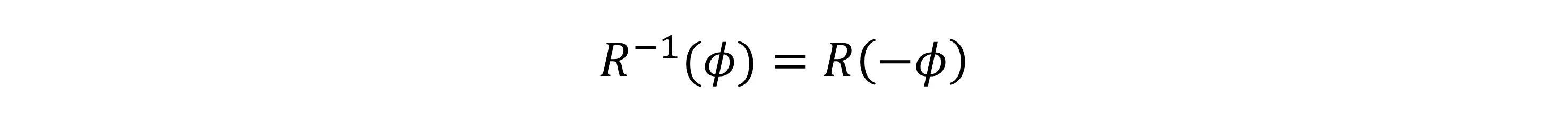
旋转矩阵是正交矩阵,其行列式始终为1;
缩放变换
设缩放因子为 s,则沿坐标轴的缩放变换矩阵可写作:
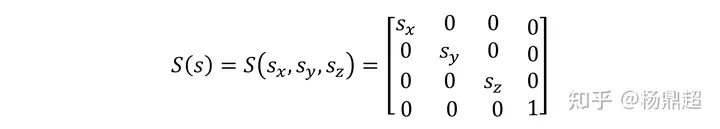
若缩放因子的三个分量相等,则称之为均匀缩放,否则为非均匀缩放。缩放矩阵的逆,就是取缩放因子的倒数:
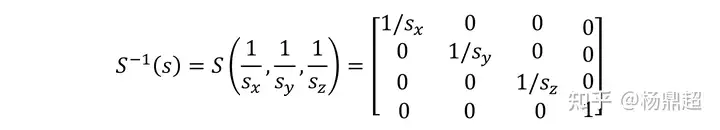
三维空间中绕任意轴旋转推导
如图所示,我们将向量 v 绕 r 单位向量旋转一个角度,即要写出 v’ 的表达式,可考虑把 v 分解为垂直于 r 和平行于 r 方向的两个向量:

于是引入 w 向量,建立坐标系:
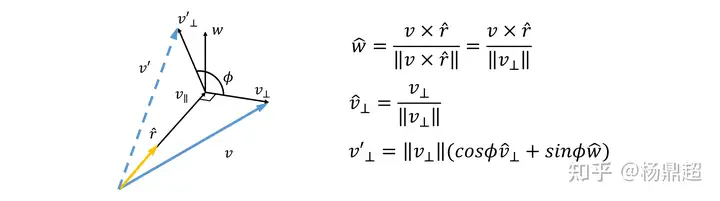
于是可把 v’ 表示出来:
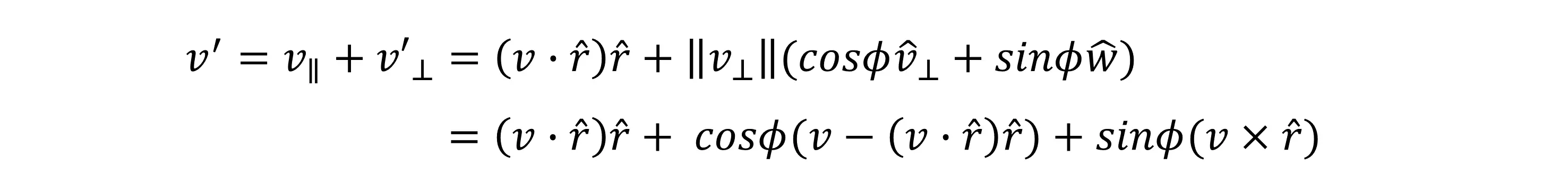
将其展开为矩阵形式:
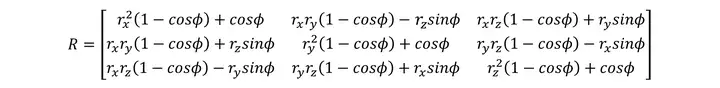
参考
https://zhuanlan.zhihu.com/p/356878461
Games101.