有向无环图
在讨论拓扑排序之前,要先知道一个重要的概念:有向无环图。
有向无环图,简称 DAG(Directed Acyclic Graph),是一种图论中的概念,它具有以下两个主要特征:
- 有向(Directed):图中的每条边都有一个方向,即每条边从一个节点指向另一个节点。例如,如果存在一条边 u→v,这表示从节点 u 指向节点 v;
- 无环(Acyclic):图中不存在任何包含多个节点的环路。也就是说,从一个节点出发,通过若干条边可以到达的其他节点中,不可能回到这个出发节点;
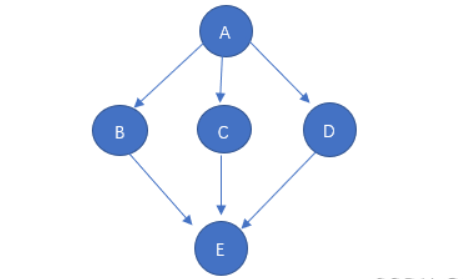
DAG 是能够进行拓扑排序的唯一图结构。因为没有环,节点可以按照依赖关系排序。
拓扑排序的思想
依赖关系的排序
拓扑排序的目标是对节点进行排序,确保在排序结果中,每个节点都在其所有依赖节点之后。也就是说,如果有一条有向边 u→v,则在排序结果中 u 必须排在 v 之前。
无环性
拓扑排序只能应用于有向无环图(DAG)。如果图中存在环(即有回路),则无法完成拓扑排序,因为环中的节点彼此依赖,无法确定一个合适的排序顺序。
入度的利用
入度表示指向某个节点的边的数量。拓扑排序从入度为 0 的节点开始,因为这些节点没有依赖关系,可以首先被处理。将一个入度为 0 的节点加入排序后,删除与该节点相关的边,并更新其他节点的入度。对于每一个入度变为 0 的节点,将其加入到下一轮排序中。
递归消除依赖
通过不断移除入度为 0 的节点及其边,图中的节点和边逐渐减少,最终所有节点都被排序,或检测到剩下的节点形成了环。
拓扑排序实现
Kahn 算法
这种方法直接使用入度的概念:
- 找出所有入度为 0 的节点,将它们放入一个队列中;
- 从队列中依次取出节点,将其加入拓扑排序结果;
- 删除该节点的所有出边,更新目标节点的入度。如果某个节点的入度变为 0,则其加入队列;
- 重复步骤 2 和 3,直到队列为空;
- 如果所有节点都被处理,则得到有效的拓扑排序;如果有节点未被处理,说明图中存在环;
DFS
通过深度优先搜索(DFS)实现拓扑排序:
- 对图中的每个节点执行 DFS,按照完成时间的逆序记录节点;
- 当 DFS 完成对某个节点的访问时,将该节点加入一个栈中;
- 最终栈中的节点顺序即为拓扑排序的结果;
- 这种方法也可以检测环,如果在 DFS 过程中遇到已经在访问中的节点,则说明图中存在环;
例题
拓扑排序的一大应用在于解决依赖问题。
题目
设计一个“包的依赖加载”算法,给定一个二维数组,其中一维代表包的索引,二维代表该包的依赖包索引(即必须先加载其依赖包才能加载该包),算法要求返回一个能让包正确加载的顺序。例如给定二维数组为[[2],[0,2],[3],[]],则代表包 0 的依赖包为包 2,包 1 的依赖包为包 0 和包 2,包 2 的依赖包为包 3,包 3 没有依赖包,所以返回的加载顺序应该是[3,2,0,1]。
解决步骤
这道题可以用基于 DFS 的拓扑排序实现:
- 将问题转化为有向图,每个包为一个节点,依赖关系为有向边;
- 使用深度优先搜索(DFS)检测每个节点是否被访问过;
- 如果某个包还没被加载,先加载它的依赖包,再加载该包;
- 确保避免循环依赖(这个问题假设依赖是无环的);
代码
#include <iostream>
#include <vector>
#include <stack>
using namespace std;
// 递归函数,使用DFS访问包,维护加载顺序
void dfs(int package, const vector<vector<int>> &dependencies, vector<bool> &visited, stack<int> &loadOrder)
{
// 标记当前包为已访问
visited[package] = true;
// 遍历当前包的依赖包
for (int dep: dependencies[package])
{
if (!visited[dep])
{
dfs(dep, dependencies, visited, loadOrder);
}
}
// 当前包的所有依赖包都已加载,将当前包加入加载顺序
loadOrder.push(package);
}
// 主算法函数
vector<int> loadPackages(const vector<vector<int>> &dependencies)
{
int n = dependencies.size(); // 包的数量
vector<bool> visited(n, false); // 记录包是否已访问
stack<int> loadOrder; // 存储加载顺序
// 对每个包进行DFS
for (int i = 0; i < n; i++)
{
if (!visited[i])
{
dfs(i, dependencies, visited, loadOrder);
}
}
// 将栈中的加载顺序转换为结果数组
vector<int> result;
while (!loadOrder.empty())
{
result.push_back(loadOrder.top());
loadOrder.pop();
}
return result;
}
int main()
{
// 输入二维数组,表示每个包的依赖包索引
vector<vector<int>> dependencies = {
{2}, // 包0依赖包2
{0, 2}, // 包1依赖包0和包2
{3}, // 包2依赖包3
{} // 包3没有依赖
};
// 调用算法计算加载顺序
vector<int> loadOrder = loadPackages(dependencies);
// 输出加载顺序
for (int pkg: loadOrder)
{
cout << pkg << " ";
}
return 0;
}解释
- 输入是一个二维数组,表示每个包的依赖包索引。
dependencies[i]表示第i个包的所有依赖包的索引; - DFS递归函数:通过深度优先搜索遍历所有包的依赖,确保在访问每个包之前,先访问它的所有依赖包;
- 结果存储在栈中:因为深度优先搜索是后序遍历(先访问依赖包,再访问自身),所以将结果存入栈中,最后再从栈中弹出生成正确的加载顺序;
示例运行:
对于输入 [[2], [0, 2], [3], []],输出将是:
3 2 0 1
即先加载包3,再加载包2、包0,最后加载包1。
算法复杂度:
- 时间复杂度:O(V + E),其中V是包的数量,E是依赖关系的数量。
- 空间复杂度:O(V),主要用于存储递归栈和结果。