概述
平衡因子
某节点左右子树的高度差
AVL树的特点
-
每个节点的平衡因子只可能是1、0、-1(绝对值 ≤ 1,如果超过 1,称之为“失衡”),所以每个节点的左右子树高度差不超过1
-
搜索、添加、删除的时间复杂度是
O(logn)
AVL树是二叉平衡搜索树
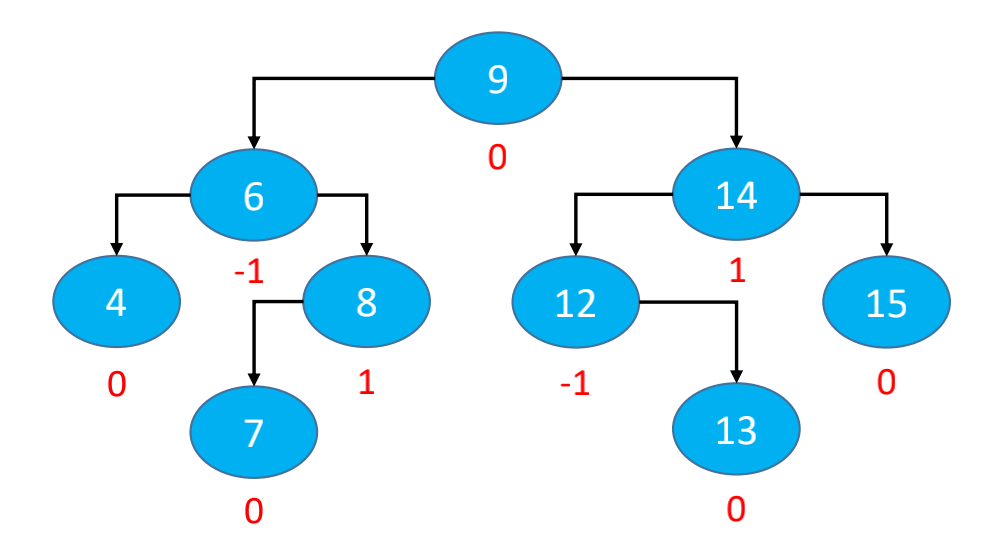
平衡对比
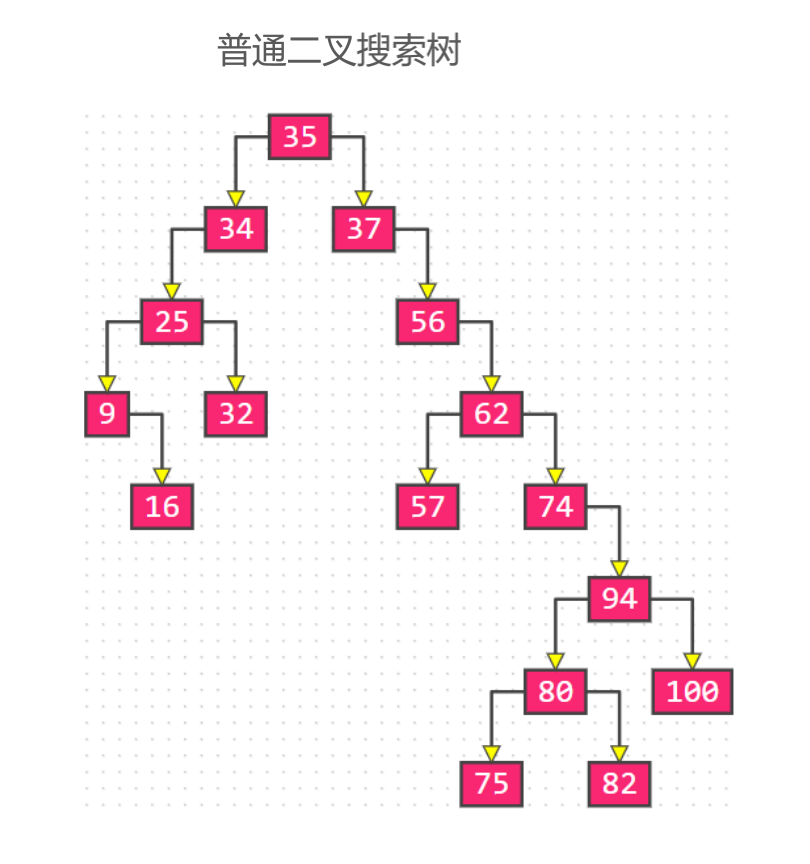
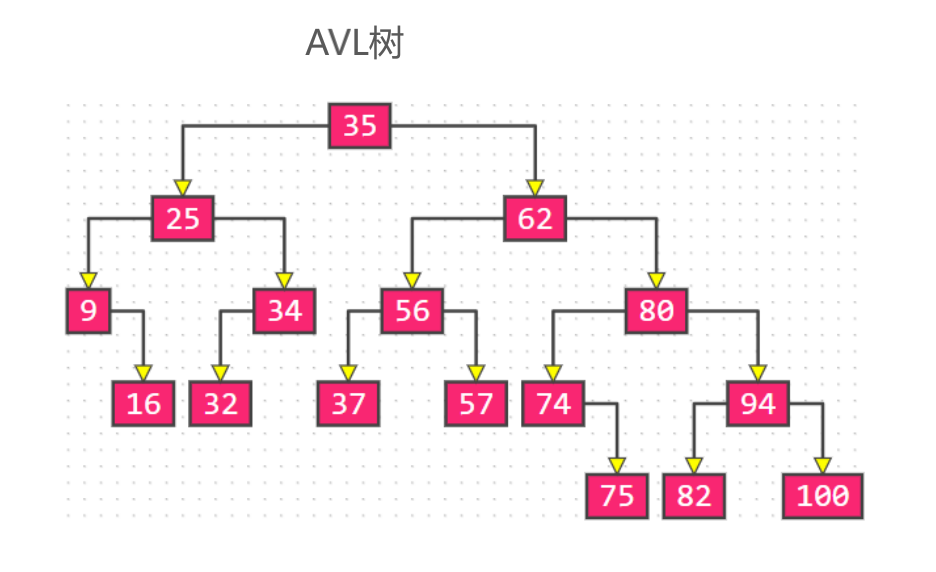
继承结构
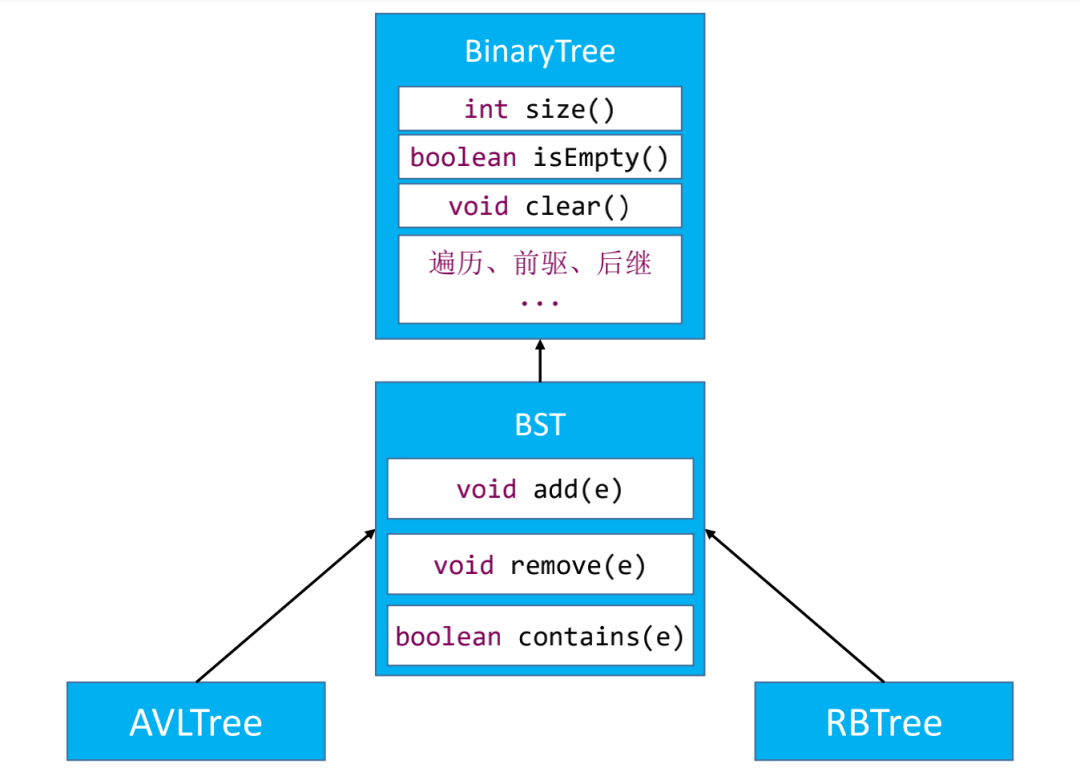
二叉搜索树继承自二叉树,而AVL树和红黑树是在二叉搜索树基础上进行的调整,所以AVL树和红黑树可以是二叉搜索树的子类;
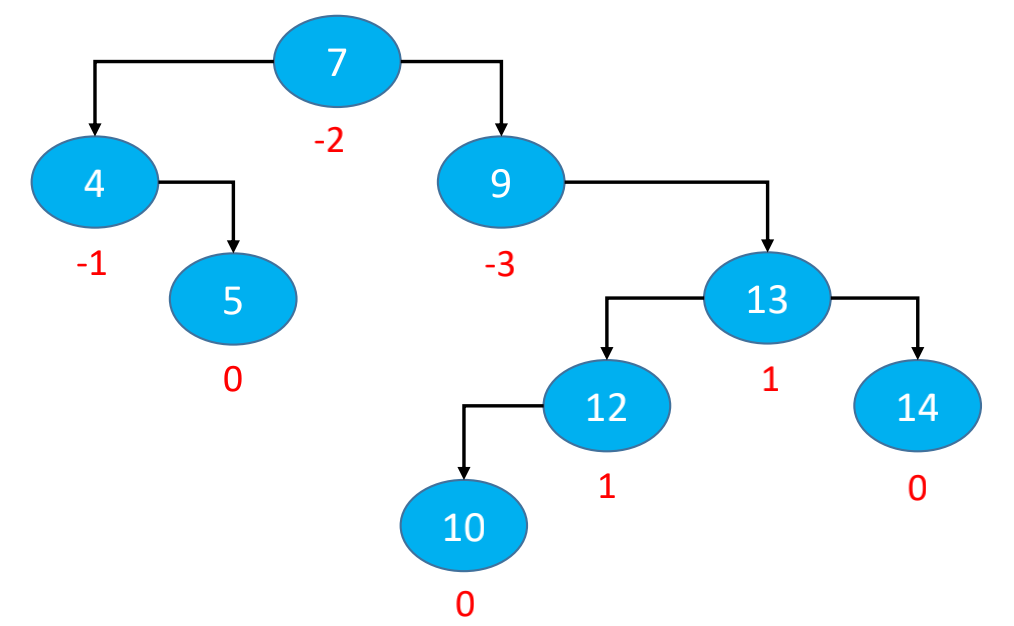
添加导致的失衡
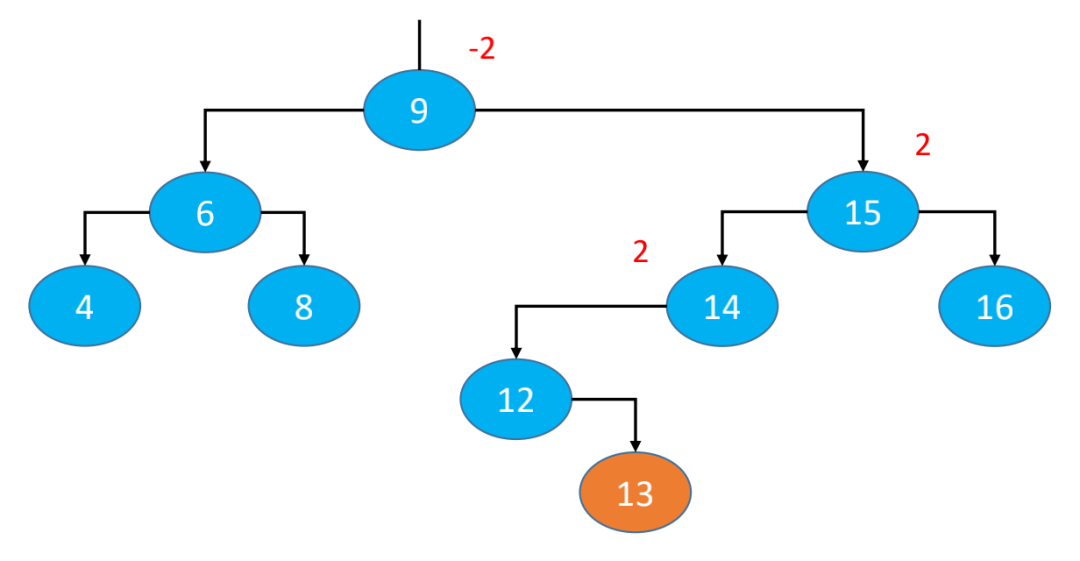
在没有添加13之前,是一棵平衡树;添加13后,节点14和节点15的平衡因子变成了2(原来是1),节点9的平衡因子变成-2(原来是-1),所以添加13后导致失衡;最坏情况是可能会导致所有祖先节点都失衡,但是父节点(节点12)和非祖先节点(节点4、6、8、16)都不可能失衡;
旋转
概述
在每一次插入数值之后,树的平衡性都可能被破坏,这时可以通过一个简单的操作来矫正平衡,这个操作就是旋转;
旋转的目的就是降低高度,通过降低整棵树的高度来平衡;哪边的树高,就把那边的树向上旋转;
所谓的左旋和右旋都是以子树为原点的:如b是a的子树,那么旋转就围绕b来进行;
-
如果b是a的左子树,那么就围绕b将a向右旋转,看着就像是a直接掉下来了,掉成了b的右子树;
-
如果b是a的右子树,那么就围绕b将a向左旋转,看着就像是a直接掉下来了,掉成了b的左子树;
插入节点时分四种情况,四种情况对应的旋转方法是不同的,例如对于被破坏平衡的节点 a 来说:
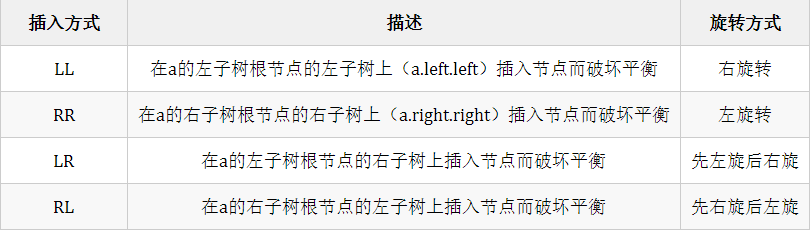
LL和RR因为只旋转一次,又称为单旋;LR和RL旋转了两次,称为双旋;
LL – 右旋转
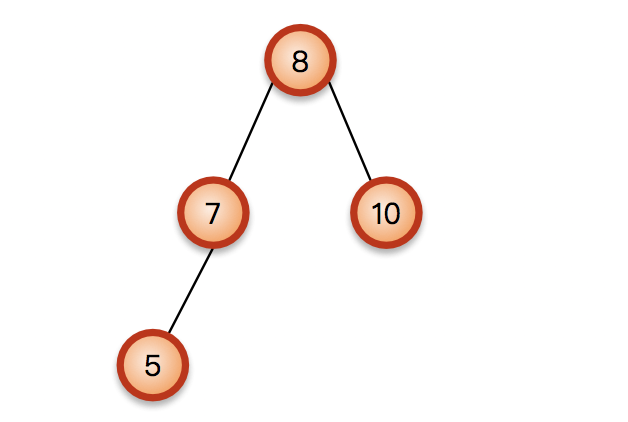
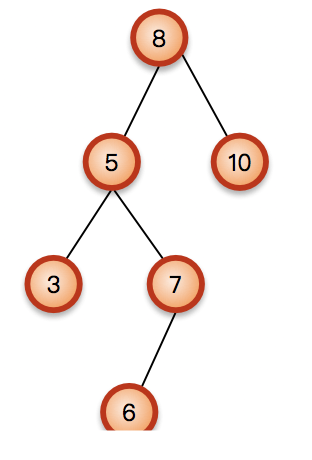
如上图一个简单的AVL树,如果在插入一个元素3,就会变成下面这样,破坏平衡;
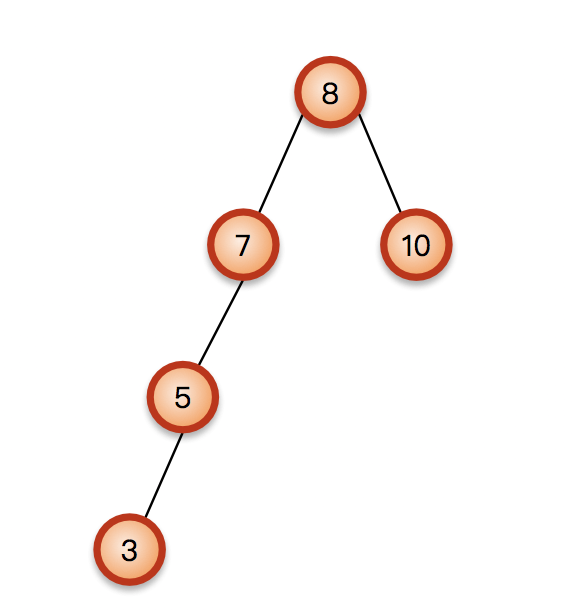
被破坏了平衡首先要找到是哪个树被破坏了平衡,然后调整这个树。然后继续往上一个一个的调整;
既然是被新插入的节点3破坏的,那么不平衡的树一定在从新插入的节点3到根节点8的路径上;找离新插入的节点最近的不平衡的树进行调整,上图中就是7;
节点7的左子树高度为2,右子树为空,高度为2 ,不平衡。根据表格要进行右旋转;
先把7这棵不平衡的树挑出来:
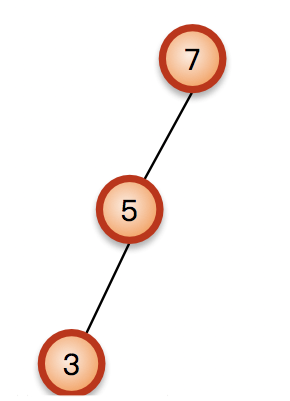
这棵树是最近的不平衡的树,把左子树5向上提一下,这时旋转就很明显了,抓着5向上一提,7就掉到5的右边了,成了5的右子树;
这个过程就是右旋:
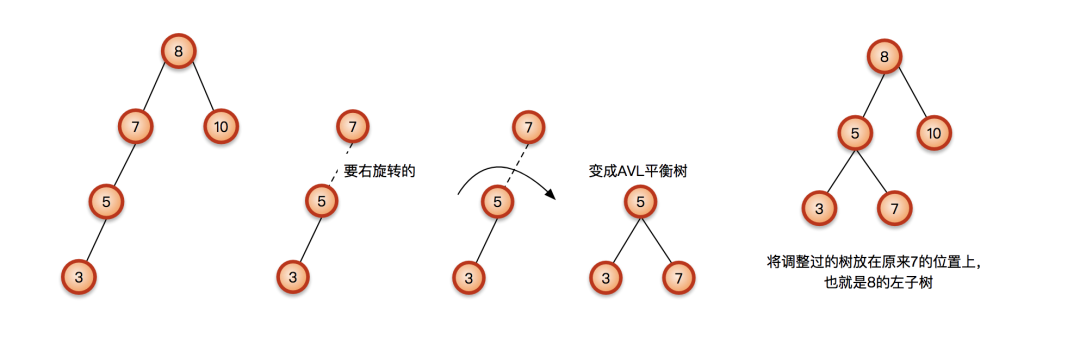
这时继续往上找,发现每个节点都符合了平衡条件,所以整棵树就变成了AVL树;
那如果节点5本来就有了右子树呢?照样右旋转,只要把原来5的右子树变成旋转后的7的左子树就行了。因为5的右子树肯定比5大,但是也肯定比7小的:
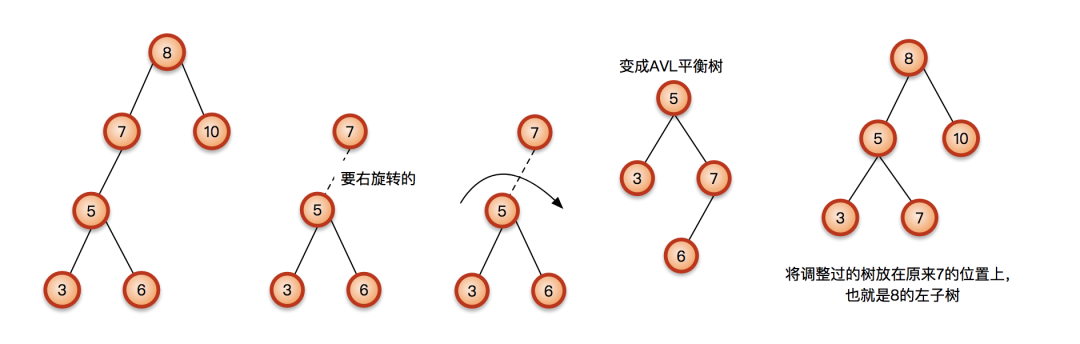
其实上面最后旋转成的树是下面这样的:
这棵树的根节点是不平衡的,还需要使用后面的双旋转来调整;使用LR先左旋后右旋调整后是这样的,具体方法看后面的;
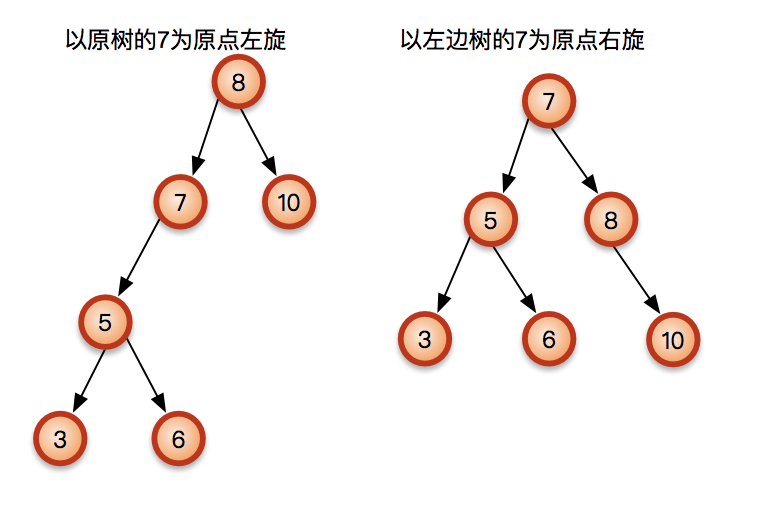
RR – 左旋转
在右子树的右子树上插入节点破坏的平衡需要左旋转来矫正;左旋转和右旋转类似,都是单旋转;
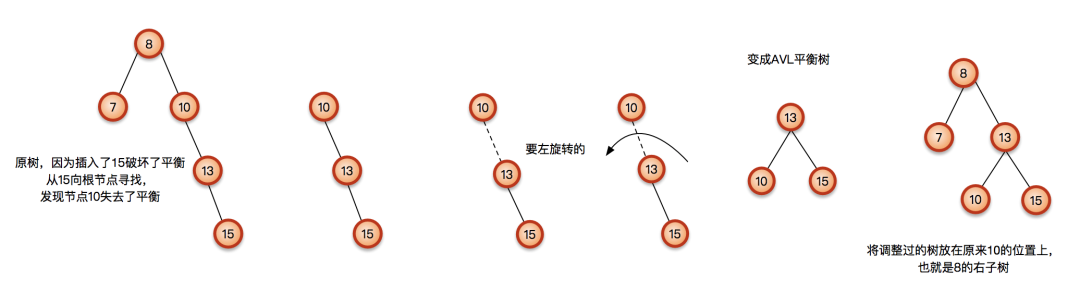
LR – 先左旋再右旋
如果在第一个例子中插入的不是3,而是6,就成了下面的样子,依然破坏了平衡;
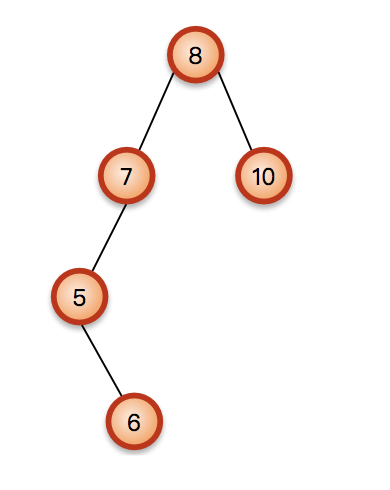
被破坏平衡的树依然是7,但是这次就不能通过一次旋转解决了,怎么转都不行。要从6开始到7进行先左旋再右旋才可以矫正平衡:
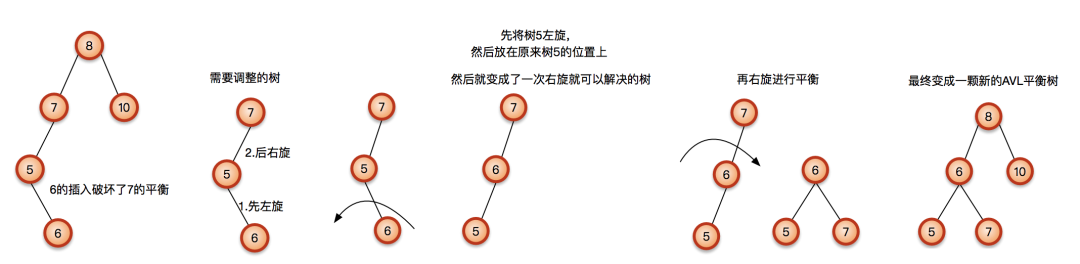
RL – 先右旋再左旋
当破坏平衡的节点是这个树的右子树的左子树时,要进行先右旋转再左旋转来矫正;
同样是从破坏平衡的那个节点开始旋转,先右旋转后左旋转:
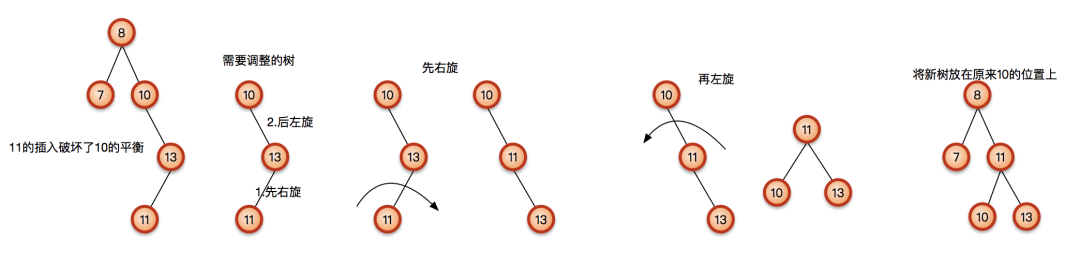
总结
添加
-
可能会导致所有祖先节点都失衡
-
只要让高度最低的失衡节点恢复平衡,整棵树就恢复平衡(仅需
O(1)次调整)
删除
-
可能会导致父节点或祖先节点失衡(只有1个节点会失衡)
-
恢复平衡后,可能会导致更高层的祖先节点失衡(最多需要
O(logn)次调整)
平均时间复杂度
-
搜索:
O(logn) -
添加:
O(logn),仅需O(1)次的旋转操作 -
删除:
O(logn),最多需要O(logn)次的旋转操作
代码
#pragma once
#include <assert.h>
template <class K, class V>
struct AVLTreeNode
{
AVLTreeNode<K, V> *_left;
AVLTreeNode<K, V> *_right;
AVLTreeNode<K, V> *_parent;
pair<K, V> _kv;
int _bf;
AVLTreeNode(const pair<K, V> &kv)
: _left(nullptr), _right(nullptr), _parent(nullptr), _kv(kv), _bf(0)
{
}
};
template <class K, class V>
class AVLTree
{
typedef AVLTreeNode<K, V> Node;
public:
bool insert(const pair<K, V> &kv)
{
if (_root == nullptr)
{
_root = new Node(kv);
return true;
}
Node *parent = nullptr;
Node *cur = _root;
while (cur)
{
if (cur->_kv.first < kv.first)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_kv.first > kv.first)
{
parent = cur;
cur = cur->_left;
}
else
{
return false;
}
}
cur = new Node(kv);
if (parent->_kv.first < kv.first)
{
parent->_right = cur;
cur->_parent = parent;
}
else
{
parent->_left = cur;
cur->_parent = parent
}
while (parent)
{
if (cur == parent->_left)
{
parent->_bf--;
}
else
{
parent->_bf++;
}
if (parent->_bf == 0)
{
break;
}
else if (parent->_bf == 1 || parent->_bf == -1)
{
cur = parent;
parent = parent->_parent;
}
else if (parent->_bf == 2 || parent_bf == -2)
{
// 旋转
if (parent->_bf == 2 && cur->_bf == 1)
{
RotateL(parent);
}
else if (parent->_bf == -2 && cur->_bf == -1)
{
RotateR(parent);
}
else if (parent->_bf == 2 && cur->_bf == -1)
{
RotateRL(parent);
}
else if (parent->_bf == -2 && cur->_bf == 1)
{
RotateLR(parent);
}
break;
}
else
{
assert(false);
}
}
return true;
}
void RotateL(Node *parent)
{
Node *subR = parent->_right;
Node *subRL = subR->_left;
parent->_right = subRL;
subR->left = parent;
Node *parentparent = parent->_parent;
parent->_parent = subR;
if (subRL)
subRL->_parent = parent;
if (_root == parent)
{
subR = _root;
subR->_parent = nullptr;
}
else
{
if (parentparent->_left == parent)
{
parentparent->_left = subR;
}
else
{
parentparent->_right = subR;
}
subR->_parent = parentparent;
}
parent->_bf == subR->_bf = 0;
}
void RotateR(Node *parent)
{
Node *subL = parent->_left;
Node *subLR = subL->_right;
subL->_right = parent;
parent->_left = subLR;
Node *parentparent = parent->_parent;
parent->_parent = subL;
if (subLR)
subLR->_parent = parent;
if (parent == _root)
{
subL = _root;
subL->_parent = nullptr;
}
else
{
if (parentparent->_left == parent)
{
parentparent->_left = subL;
}
else
{
parentparent->_right = subL;
}
subL->_parent = parentparent;
}
parent->_bf = subL->_bf = 0;
}
void RotateRL(Node *parent)
{
Node *subR = parent->_right;
Node *subRL = subR->_left;
int bf = subRL->_bf;
RotateR(parent->_right);
RotateL(parent);
if (bf == 0)
{
parent->_bf = subR->_bf = subRL->_bf = 0;
}
else if (_bf == -1)
{
parent->_bf = 0;
subRL->_bf = 0;
subR->_bf = 1;
}
else if (_bf == 1)
{
parent->_bf = -1;
subRL->_bf = 0;
subR->_bf = 0;
}
else
{
assert(false);
}
}
void RotateLR(Node *parent)
{
Node *subL = parent;
Node *subLR = subL->_right;
int bf = subLR->_bf;
RotateL(parent->_left);
RotateR(parent);
if (bf == -1)
{
parent->_bf = 1;
subLR->_bf = 0;
subL->_bf = 0;
}
else if (bf == 1)
{
subLR->_bf = 0;
subL->_bf = -1;
parent->_bf = 0;
}
else if (bf == 0)
{
parent->_bf = 0;
subL->_bf = 0;
parent->_bf = 0;
}
else
{
assert(false);
}
}
private:
Node *_root = nullptr;
};
参考链接
https://www.modb.pro/db/145886
https://blog.csdn.net/m0_74092462/article/details/140000387